Quicklinks

• There are none, suggest some!

Overview

When working with Revit areas, either through an area scheme or architectural rooms, it’s common to create a schedule of those areas, and utilize the auto-calculation aspect of Revit to get the totals of the floor/department/etc.

Problem

If you interrogate your list of rooms, occasionally you will notice that the rounded values presented in the schedule end up not adding up to the totals presented in the schedule. There ends up being a discrepancy between some values, which can cause issues for clients or in planning.

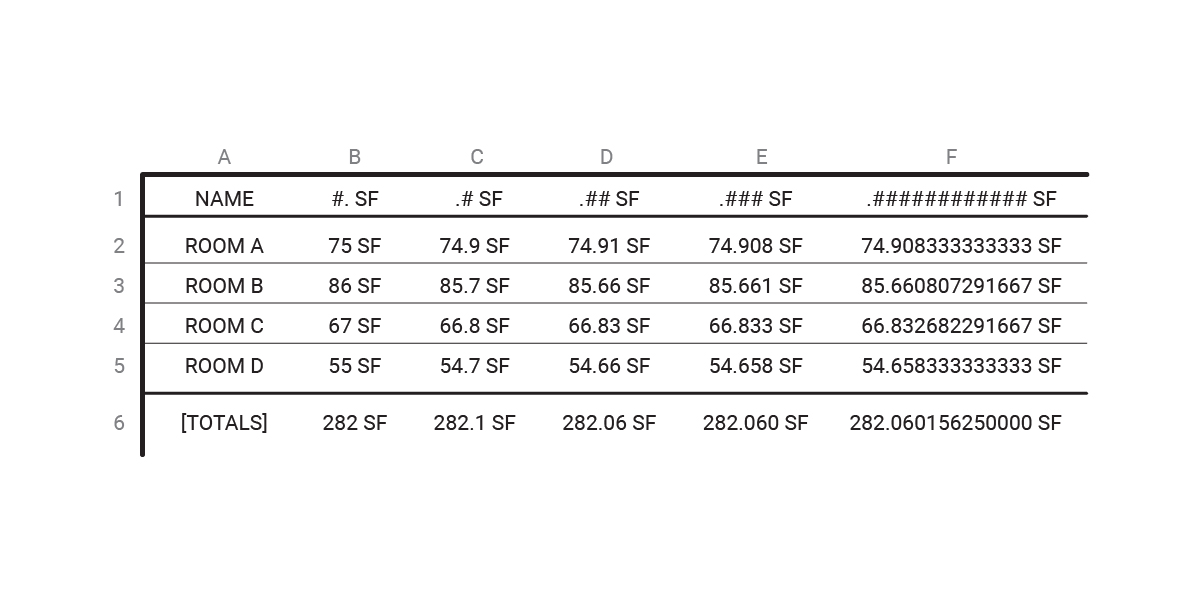
Example

To illustrate and discuss what is happening, we will use this example. Presented here are 4 rooms that were created in Revit, and the values associated with the rounding created in a schedule from Revit. Each column B through F was set to the Area of the space/room, with different rounding precision for each (0 decimals, 1 decimal, etc)

Maximum Precision – Column F

While we have read elsewhere that Revit stores 15 decimals for numbers, it only lets you schedule up to 12 decimals for the Area in a Room or Area schedule (done by “custom” with .000000000001 precision).

Therefore, we are stating that 12 decimals is the “maximum precision” you can get in an Area/Space; and when we discuss the “most precise” area measurement, this is the precision we are talking about (column F).

Issue

How Revit Rounds Spaces & Rooms

The main issue here is that Revit is rounding the most precise value it has for the room/space. It rounds this precise value to the exact specified rounding (1,2,3 decimals, etc).

The presented rounded values (Columns B, C, D, E) are simply rounded values, and not stored within the program. Therefore, they are not the values that get added together for the total.

Total Values

Instead, to maintain accuracy, Revit is adding together the precise room values (Column F) and then rounding this value. This presents the most precise value it can for the Total Area because it is waiting until the last moment to round. This keeps the significant digits to 12 decimal places in the equation, until the final rounding to the decimal precision requested. This means that the value is more precise, but may not match the values of your rounded totals.

Example Discrepancy

We chose this dataset because it can illustrate this issue. If you add up Column B rooms, you will get a value of 283 SF, while the actual rounded value is 282 SF. While minimal, this is still a discrepancy of 1 SF across 4 rooms.

The discrepancy is not limited to 1SF, and can increase; as an example, if we were to double the rooms to the exact same size, Revit’s tabulated total becomes 564 SF across 8 rooms, while the calculated total from the rounded values is 566 SF. This is a difference of 2 SF (double the earlier value).

Decimals

While the decimals in our example for .1, .01 and .001 precision all are accurate to the totals, this is not always the case. Obviously, by its nature, the more precise values will be closer to the actual totals regardless, but there is the possibility that these are all off as well.

What’s actually happening

It generally depends on how many areas you have, and the distance to “5” (as this is the rounding cutoff) for the value of the decimal you want.

For example 4 spaces

• Values of .949 for 4 values will equal a total of 3.796. This rounds to 3.80 for 2 decimals.
• The 2 decimal value of .95 * 4 is equal to 3.80. This matches.

However, if we look at 5 spaces with this value.

5 spaces

• Values of .949 for 6 values will equal a total of 5.694. This rounds to 5.69 for 2 decimals.
• The 2 decimal value of .95 * 6 = 5.70 

Typical Values Balanced by Probability

This is an extreme example. Typically, while .49 values are low, they are normally balanced out by various .51+ values that are high. Therefore, while its possible, its unlikely that your values are off by ‘that’ much ever.

Workaround

Let’s say that you do want the total to represent an addition of the values that have been rounded. This is possible using a calculated parameter in your schedule, and hiding the ‘actual’ area value. Keep in mind that if you do a workaround, you are actually presenting a ‘less precise’ value as your total.

Calculated Parameter

1. Create a new calculated parameter. The type needs to be “Area”.
2. Decide on the precision you want, and copy/paste the corresponding precision formula in (below).
3. Make sure to set the Area parameter to be a ‘hidden value’
4. Make sure to set the “Field Format” of the new calculated parameter to match your precision you set. It will default to your ‘projects’ precision.

Formulas

Follow the formulas below for each precision level you want. For more precision, follow the pattern below.

Essentially what you are doing is multiplying the most precise value by a certain amount, to get the precision you want to be at the integer level. Then you are rounding that value to the nearest integer. Once you get that rounded value, you are then dividing by the amount you multiplied by in order to get back to a decimal amount. All the dividing and multiplying of SF are to resolve the units.

Precision	Formula
0 decimal places	((round((Area * 1) / 1 SF)) * 1 SF) / 1
1 decimal places	((round((Area * 10) / 1 SF)) * 1 SF) / 10
2 decimal places	((round((Area * 100) / 1 SF)) * 1 SF) / 100
3 decimal places	((round((Area * 1000) / 1 SF)) * 1 SF) / 1000